👨🏻‍💻 Ilya B.

CLASS 004 - Queues, Trees

4 min read

Queue

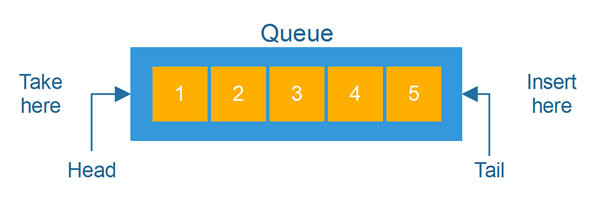
//queue in js
class Node {
    constructor(value) {
        this.value = value;
        this.next = undefined;
        this.prev = undefined;
    }
}
 
class Queue {
    constructor() {
        this.head = undefined;
        this.tail = undefined;
        this.length = 0;
    }
 
    enqueue(item) {
        const node = new Node(item);
        this.length++;
        
        if (!this.tail) {
            this.head = this.tail = node;
            return;
        }
        
        node.prev = this.tail;
        this.tail.next = node;
        this.tail = node;
    }
 
    deque() {
        if (!this.head) return undefined;
        
        const head = this.head;
        this.head = this.head.next;
        
        if (this.head) this.head.prev = undefined;
        else this.tail = undefined;
        
        this.length--;
        return head.value;
    }
 
    peek() {
        return this.head ? this.head.value : undefined;
    }
}

Tree

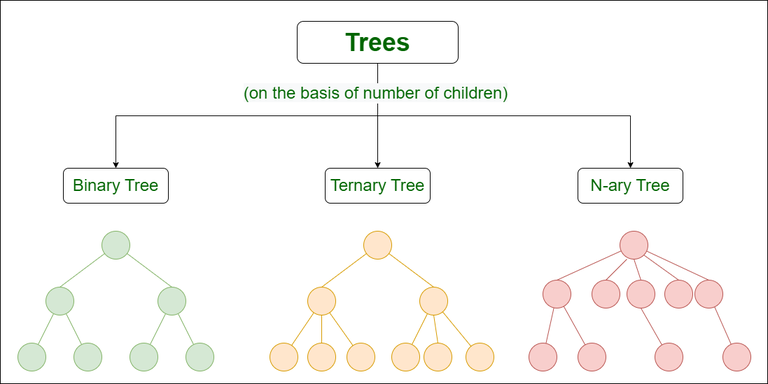
We sometimes need to represent data that is hierarchical for which we need a tree structure. For instance, a use case could look like a phone number extension management system, a file folder structure, or a decision tree. The there are methods for traversing the tree, adding, removing or replacing items.

We firs have to define some basic elements:

      A 
     / \ 
    B  C 
    / \ \ 
    D E F
  • Root node: this is the starting node.
  • Parent & Child Nodes: the relationship between a given node and nodes beneath it.
  • Sibling Nodes: nodes at the same level, with the same parent.
  • Leaf nodes: the nodes at the end, with no children.
  • Edge: the metaphorical line connecting the parent and child node.
  • Tree height: the longest path from root node to leaf node.
  • Tree depth: the path from the root node to the given node.

Some more definitions

  • A binary tree has two nodes per parent.
  • an n-ary tree has n nodes per partent.
  • A full tree has all levels filled VS a complete tree has all but the last level filled.
  • A balanced tree means the length of the left and right subtrees the same or different by one level maximum.

Binary Search Tree

This binary tree follows a special structure. all items on the left subree are less than the root node and all items on the right subtree are greater than the root node. This enables efficient searching.

Let’s start by defining a node:

class Node {
    constructor(value) {
        this.value = value;
        this.left = null;
        this.right = null;
    }
}

In this case it starts to resemble a linked list - because it is in a way.

Traversal

OK so we know that the node has to traverse the tree. How does it do so?

visitNode()
recurse() //LEFT or RIGHT with recurseLeft() or recurseRight()

The order in which it does these operations is useful to know to be able to apply the correct one for the best performance in a given context. There are three conventional ways to do it:

  • Pre-Order First visit the node, then recurse.
  • In-Order First recurse left, then visit the node, then recurse again.
  • Post-order Recurse left, then right, then visit the node.
         8
        /  \
      24     4 
     / \    /  \
    6   5  22   7

[8, 24, 6, 5, 4, 22, 7] //- Pre-order
[6, 24, 5, 8, 22, 4, 7] //- In-order 
[6, 5, 24, 22, 7, 4, 8] //- Post-order

Q: What is the running time of these traversals?

Answer: O(n)

Ok so let’s do a pre-order walk:

function walk(pointer, path) {
    if (!pointer) {
        return path;
    }
    path.push(pointer.value);
    walk(pointer.left, path);
    walk(pointer.right, path);
 
	return path;
} //curr is a Node that is a number

We can test a simple version in the browser console:

//this simple version is inelegant, but works to demonstrate
class Node {
	constructor(value, left = null, right = null) {
		this.value = value;
		this.left = left;
		this.right = right;
	}
}
 
let path = [];
function walk(pointer) {
	try {
		walk(pointer.left);
	} catch (error) {
		path.push(pointer.value);
		walk(pointer.right);
	}
}
//here, the catch block error propagates up the call stack forcing the tree traversal to complete itself
 
//test with some nodes
nodeD = new Node(6);
nodeE = new Node(5);
nodeF = new Node(22);
nodeG = new Node(7);
nodeC = new Node(4, nodeF, nodeG);
nodeB = new Node(24, nodeD, nodeE);
nodeA = new Node(8, nodeB, nodeC);
//log the path afterwards
console.log(path);

This type of traversal is called depth-first search. And because we are doing recursion, we are implicitly using a stack.

Comparing Trees

function compare(a, b) {
	
	if (a === null && b === null) {
		return true;
	}
	if (a === null || b === null) {
		return false;
	}
	if (a.value !== b.value) {
		return false;
	}
 
	return compare(a.left, b.left) && compare(a.right, b.right);
	}
}
To be covered next class:
- Breadth first Seach
- Depth-First Find
- Depth-first Insert
- Depth-first Delete

Exercises

Filter by javascript and easy to start

Queue

https://leetcode.com/problem-list/queue/

Tree

https://leetcode.com/problem-list/binary-tree/

Graph View