đŸ‘šđŸ»â€đŸ’» Ilya B.

CLASS 001 - Big O Complexity, Arrays, Linked Lists, Linear Search, Binary Search

6 min read

Objective: familiarize the class with the fundamentals of an Array

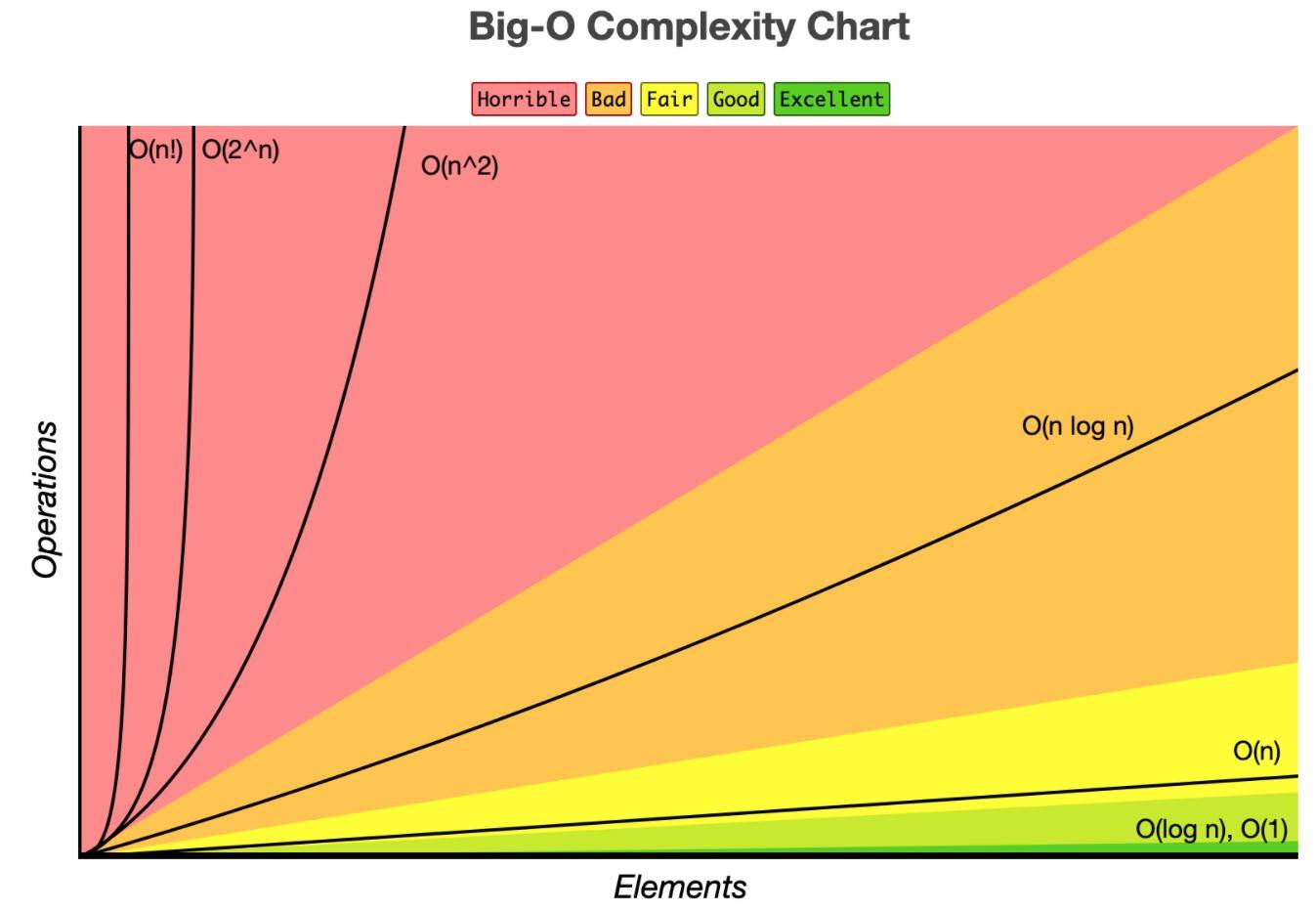
Big O Complexity:

What’s the running time of this function?

// Linear growth illustrated
// For every additional character in the string, the loop has to iterate one more time
function sumCharCodes(n) {
    let sum = 0;
    for (let i = 0; i < n.length; ++i) {
        sum += n.charCodeAt(i);
    }
    return sum;
}
 
> sumCharCodes("test");
448

Trick: look for loops

What’s the running time of this function?

function sumCharCodes(n) {
    let sum = 0;
    for (let i = 0; i < n.length; ++i) {
        sum += n.charCodeAt(i);
    }
    for (let i = 0; i < n.length; ++i) {
        sum += n.charCodeAt(i);
    }
    return sum;
}

This is still O(n)! because we drop constants!

Why we drop constants:

N = 1, O(10N) = 10, O(N^2) = 1 

N = 5, O(10N) = 50, O(N^2) = 25 

N = 100, O(10N) = 1,000, O(N^2) = 10,000 // 10x bigger 

N = 1000, O(10N) = 10,000, O(N^2) = 1,000,000 // 100x bigger 

N = 10000, O(10N) = 100,000, O(N^2) = 100,000,000 // 1000x bigger

What’s the running time of this function?

function sumCharCodes(n) {
    let sum = 0;
    for (let i = 0; i < n.length; ++i) {
		const charCode = n.charCodeAt(i);
		if(charcode === 69){
		// CAPITAL E
			return sum;
		} 
		sum += charCode;
    }
    return sum;
}
 
// Worst case: any string with the letter E will terminate early except if it is the last item in the list. 
// Scenario: E one unit from the end, or two units from the end?

Important concepts

  1. Growth with respect to the input
  2. Constants are dropped
  3. Interviewers care about the worst case scenario

Big O complexity Big O Summary Table

Arrays

An array is a contiguous memory space composed of bytes. It is interpreted by the type we decide. So for example we take 4 bites and decide to interpret these as a number, that is actually a 32 bit array. So an array is zero or more pieces of memory that are understood as a type.

import java.util.Arrays;
 
public class Main {
  public static void main(String[] args) {
    int[] myIntArray = new int[3];
    System.out.println(Arrays.toString(myIntArray));
    
    myIntArray[0] = 1;
    System.out.println(Arrays.toString(myIntArray));
 
    //myIntArray[3] =4;
    //System.out.println(Arrays.toString(myIntArray));
  }
}

So in a more traditional language like Java you can do this: a = int[3] so now you have an array of length 3 x 4 bytes and a[0] is the first 4 bytes.

//at each step, log the results of a, a8 and a16
const a =  new ArrayBuffer(6);
const a8 = new Uint8Array(a);
a8[0] = 42;
const a16 = new Uint16Array(a);
a8[2] = 45;
a16[2] = 45;
a16[2] = 0x4545;

Figure

Key Takeaways:

  • Arrays are an allocation of memory of a fixed size, in a sequence, such that one can ‘walk’ the array. We will use this knowledge to build understanding of an arrayList
  • Arrays are not Lists.
  • Getting at a specific index, insertion at a specific index, deletion at a specific index. These are constant time operations because of the index.
  • Cannot grow.

Further Reading

The ArrayBuffer , Typed Array and DataView are objects that are used to represent a raw binary data buffer. A raw binary data buffer is a memory storage space that holds binary data directly, without any interpretation or processing. It is a sequence of bytes, akin to a list of numbers, that can be used to store data for further manipulation or transfer, such as image data, network resources, or decoded media streams.

// To access the node environment by typing 'node' into your terminal
// At any point, you can run 'console.log' on an item to view it
// To initiate a Typed Array:
const arrayBuffer = new ArrayBuffer(8); //this creates an array of 8 bytes in memory
const arrayBufferInt16View = new Uint16Array(arrayBuffer); // this is a 'view' of the array as a uint16array, in shared memory. 
 
> console.log(arrayBufferInt16View);
Uint16Array(4) [0, 0, 0, 0] 
 
// A `Uint16Array` views an `ArrayBuffer` as an array of 16-bit (2 bytes)

Uint16Array:

  • Each element in a Uint16Array uses 16 bits (2 bytes) to represent one data point.
  • Since it’s an unsigned integer array, it can hold values ranging from 0 to 65535.
  • The data is stored in contiguous blocks of 2 bytes for each integer in the ArrayBuffer.
// We can view the binary representation with this function
function toBinaryString(uint16Array) {
	return Array.from(uint16Array).map(num => {
 
	// Convert number to a 16-bit binary string
	let binaryStr = num.toString(2);
	return binaryStr.padStart(16, '0'); // Ensure it's 16-bits with leading zeros
	});
}
 
> console.log(toBinaryString(arrayBufferInt16View)); // Outputs the binary strings
[
  '0000000000101010',
  '0000000000000000',
  '0000000000000000',
  '0000000000000000'
]

Linked Lists

What sucks about an array?
  • Deletion (why?)
  • Insertion (why?)
  • it is ungrowable (why?)

A linked list is a series of Nodes that point to the next Node. They can be singly or doubly linked.

// Pseudocode representing a node
Node<t>
	val:T
	next?: Node<T> //singly linked list
	prev?: Node<T> // doubly linked list

example insertion of F ⇒ these are constant time!

Linear Search

class Solution {
    linearSearch(array, target) {
        // Loop through all elements in the array
        for (let position = 0; position < array.length; position++) {
            // Check if the current element is equal to the target
            if (array[position] === target) {
                // Return the index of the found element
                return position;
            }
        }
        // Return -1 if the target is not found
        return -1;
    }
}
 
const myArray = [5, 3, 8, 6, 1];  // Example array
const target = 8;  // Target to find
const sol = new Solution();
const result = sol.linearSearch(myArray, target);
console.log("Element found at index:", result);

Binary Search

class Solution {
    binarySearch(array, target) {
        let left = 0;
        let right = array.length - 1;
 
        while (left <= right) {
            let middle = Math.floor(left + (right - left) / 2);
 
            if (array[middle] === target) {
                return middle;  // Target found, return its index
            } else if (array[middle] < target) {
                left = middle + 1;  // Target is on the right half
            } else {
                right = middle - 1;  // Target is on the left half
            }
        }
        return -1;  // Target not found
    }
}
 
let solution = new Solution();
let myArray = [1, 3, 5, 7, 9];
let target = 7;
let result = solution.binarySearch(myArray, target);
console.log("Element found at index:", result);

Graph View